Statics Problem

Ropes, Rods, Force and Torque

The system shown is at rest. The rod is uniform, 120kg and 1.1m long. Rope 2 is perpendicular to the rod and rope 3 is perfectly horizontal. The base of the rod is held to the ground by a frictionless, light hinge.

Find the tension in the ropes.

As the mass is stationary, the tension in rope 4 must exactly balance its weight. Thus, T₄=2000N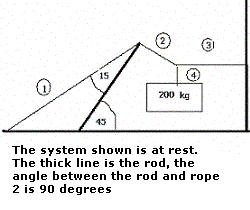

The junction between the three ropes is also stationary, so the vertical component of T₂ must also be 2000N. From the geometry of the situation, it can be seen that this component is T₂sin(45^o).

Thus, T₂=2800N.

The horizontal component of this tension must also cancel the force from the tension in the 3rd rope. T₃=T₂cos(45^o)=2000N.

To find the tension in rope one, we cannot use plain forces acting on the rod as the forces applied by the hinge on the rod are unknown and impossible to calculate without knowing T₁. However, by looking at the torque about the hinge we can eliminate these unknowns!

As the rod is neither moving or rotating, the net torque about the hinge must be zero.

T₁Lsin(15^o)-T₂L=0

T₁=T₂/sin(15^o)

T₁=11000N