Vectors in Two-Dimensional (2-D) Coordinate Systems

Cartesian and Polar Coordinates

Cartesian Coordinates (x,y): A vector, V, in a 2-D Cartesian coordinate system can be written as:

V=(V_x,V_y)=V_xi V_yj

where V_x and V_y are referred to as the vector components and i and j are unit vectors - vectors of length one - in the x and y directions respectively.

The magnitude of V is:

|V|=√(V_x² V_y²)

Polar Coordinates (r,θ): Written in polar coordinates,

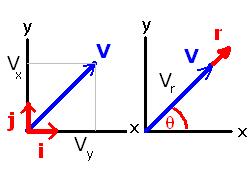
V=(V_r,V_θ)=V_rr

where r is a unit vector in the r direction (at an angle of θ counter-clockwise from the x-axis).

Relations between Cartesian and polar coordinates:

V_r = √(V_x² V_y²)

V_θ=tan^-1(V_y/V_x)

V_x = |V|cos(θ)

V_y = |V|sin(θ)